978. Get
a tree
A connected
undirected graph without loops or multiple edges is given. It is allowed to
delete edges from the graph. The goal is to obtain a tree.
Input. The first line contains two
integers – the number of vertices n (1 ≤ n ≤ 100) and the number
of edges m in the graph. The following m pairs of integers each
represent an edge. It is guaranteed that the graph is connected.
Output. Print n – 1 pairs of
integers – the edges that form a tree. The edges can be printed in
any order.
|
Sample
input |
Sample
output |
|
4 4 1 2 2 3 3 4 4 1 |
1 2 2 3 3 4 |
SOLUTION
graphs – depth first search
Algorithm analysis
Perform a depth-first
search starting from the first vertex. Build the depth-first search tree and print
all of its edges.
Example
The graph given in the
example has the following structure:
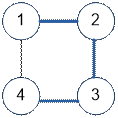
When the depth-first
search is started from vertex 1, the traversal will go through the edges: (1, 2), (2, 3),
(3, 4).
Algorithm implementation
The adjacency matrix of
the graph is stored in the array g.
#define MAX 101
int g[MAX][MAX], used[MAX];
The dfs
function performs a depth-first search starting from vertex v.
Each edge (v, i) that is part of the depth-first search tree is printed.
void dfs(int v)
{
int i;
used[v] = 1;
for(i = 1; i
<= n; i++)
if (g[v][i]
&& !used[i])
{
printf("%d
%d\n",v,i);
dfs(i);
}
}
The main part of the program. Read the input data.
scanf("%d %d",&n,&m);
memset(g,0,sizeof(g)); memset(used,0,sizeof(used));
while(m--)
{
scanf("%d
%d",&a,&b);
g[a][b] = g[b][a] = 1;
}
Start a depth-first search from the first vertex.
dfs(1);
Java implementation
import java.util.*;
public class Main
{
static int g[][],
used[];
static int n, m;
static void dfs(int v)
{
used[v] =
1;
for(int i = 1;
i <= n; i++)
if (g[v][i] ==
1 && used[i] ==
0)
{
System.out.println(v + "
" + i);
dfs(i);
}
used[v] =
2;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
g = new int[n+1][n+1];
used = new int[n+1];
for(int i = 0;
i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = g[b][a] =
1;
}
dfs(1);
con.close();
}
}